「渦とサメとコンピューター」
理工学部機械工学科 教授 大上芳文
明日の天気を計算するのに何日もかかっていたコンピューターは,飛躍的にその能力が向上し,その結果,明日の天気は明日までに予測できるようになり,テレビやラジオなどでその情報を日常的に見聞きするようになった.
「京」に代表される日本のコンピューターは,世界1,2位の座を争う高性能になっているが,しかし,未だコンピューターが不得手とする対象が存在し,それはその形状が時間的に変形する物体の周りの流れの解析である.例えば,羽ばたきながら飛ぶ鳥や蝶々,尾ひれをくねらしながら泳ぐ魚などの解析は不得手であり,計算に多大な時間がかかる.なぜなら,コンピューターで流れを計算するには,物体の表面とそれを取り囲む空間の中に,数万から数億個の多くの点を規則的に配置し,それらの計算点の上で流体の速度や圧力などの運動方程式の解を計算するのであるが,物体が変形する場合,解の精度を保つことを保証しながら,逐一,計算点を配置し直す必要があるからである.この作業に多大な時間を消費する.
このような計算点を用いないで,流体の運動方程式を解く方法に境界要素法がある.これは例えば,鍋の表面の2次元的な温度分布が分かれば,鍋の内部の3次元的な温度分布が計算できるという方法である.この手法は流体の解析にも応用することができ,物体の表面の何らかの物理量が分かれば,物体から離れた空間の物理量,すなわちこの場合は流体の速度や圧力が計算できることになる.したがって,先ほど述べた計算点を空間内に配置する必要はない.また,物体が変形しても問題はない.
何十年も前から流体解析に上述の境界要素法が用いられているが,曖昧な取り扱いがされている物理量があり,それは渦である.渦と言えば,竜巻,乱気流,渦潮などが一般的に思い出されると思うが,流体力学ではある点での流体の回転の度合いを表す物理量であり,渦度と呼ばれる.空間内での回転にはx軸周り,y軸周り,z軸周りの3つの回転があるため,渦度はその3成分を持つベクトルである.ところがこれまでの国内外の研究では,渦度がベクトルであることが曖昧にされていた.
当研究室の研究テーマは,マイクロガスタービンの開発や大気圏に突入する宇宙船の解析など広範囲にわたり,常時10テーマほどあるが,そのうちの一つは,この曖昧さをなくし,明快な方法を構築することである.その結果,物体表面,および空間内に渦度の3成分を明確に分離し,すべての必要な方程式を定式化し,解を求める手法の構築に成功した*.本方法の利点を示す簡単な計算例としては,回転球がある.これまでの方法では,どの軸の周りに球が回転しているかが明確に示せなかったが,本方法では容易である(図1).また,回転球に作用する揚力の計算も正確に行える.
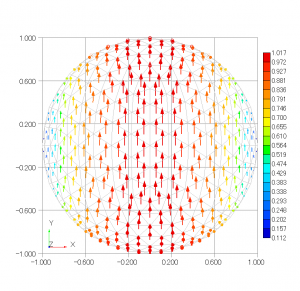
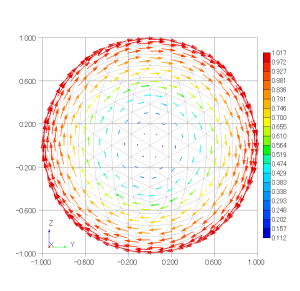
(a) 正面図 (b) 側面図
図1 静止流体中で回転する球の表面速度ベクトル
既述のように,本方法の大きな利点は変形する物体を扱えることである.その1例としてホオジロザメの泳ぐ様子を解析した結果を図2に示す.これはサメの表面の圧力分布を多色で示しており,これを積分することでサメの推進力や流体の抵抗力が計算できる.ちなみにサメの表面は4884枚の三角形のパネルで表している.
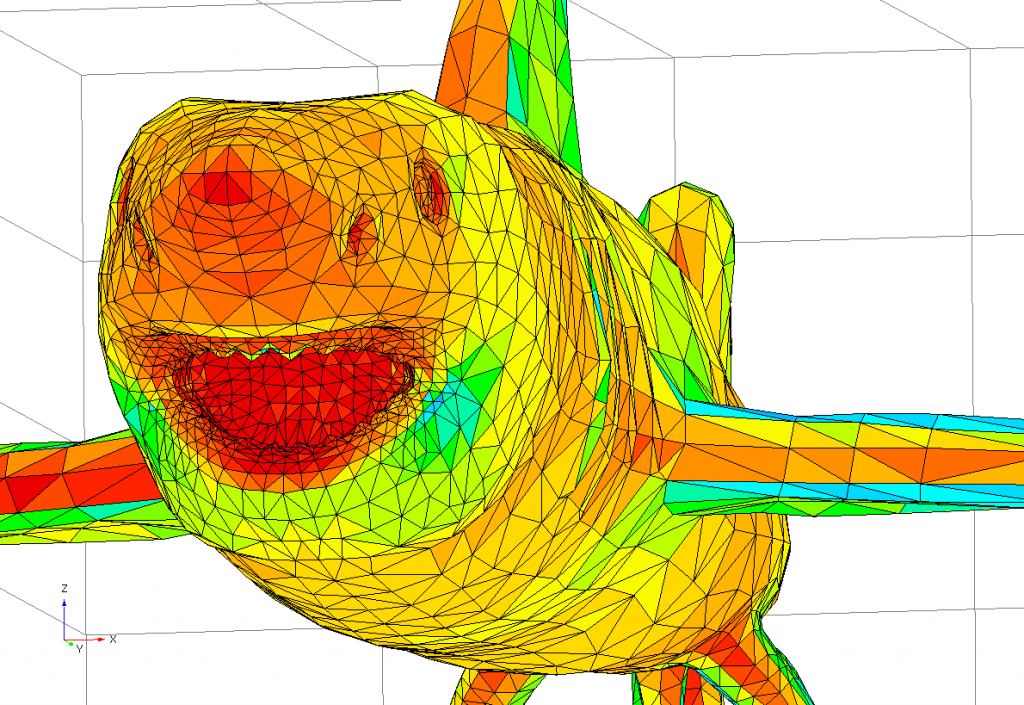
図2 泳ぐホオジロザメの表面圧力分布
このように,変形する物体の解析が行えるようになれば,鳥や蝶々の飛翔や魚の遊泳を流体力学的に解析,およびその効率化のメカニズムを解明することが出来,その結果を工学的に応用し,より斬新で効率的な推進装置や発電機の開発に繋げることができる.
* Y. Ogami, A three-dimensional source-vorticity method for simulating incompressible potential flows around a deforming body without the Kutta condition, Computers & Fluids, Volume 154, 1 September 2017, Pages 184-199



